Composing Reinforcement Learning Policies, with Formal Guarantees
or obtaining formal guarantees by synthesizing two-level controllers from verified reinforcement learning policies
This blog post is based on our recent AAMAS paper, Composing Reinforcement Learning, with Formal Guarantees.
In this blog post, I will explain how to exploit learned world models to produce agent’s controllers from carefully designed reinforcement learning policies, with formal guarantees. Let’s start with a bit of background and motivations.
Motivating Example
Consider an agent that needs to deliver a package in a warehouse amid moving obstacles. Such obstacles may consist of humans, forklifts, or other robots. In such a setting, it is critical to guarantee the agent avoids the moving obstacles and delivers its package as fast as possible, both for supply chain reliability and safety reasons.

Another option is to use model-based techniques: build a model of the environment by listing all possible agent’s actions in every environment’s state as well as their subsequent transitions. Then, planning algorithms can be used to find the best policy. However, creating such a model is challenging: one has to consider all possible interactions, including those with uncertain moving obstacles. Plus, as the warehouse gets larger, the model becomes huge, and standard planning methods might struggle to scale.
It remains learning algorithms, that would allow the agent to learn through interactions how to behave optimaly in the environment. However, it is unclear how to provide guarantees with machine learning algorithms, especially on the way the agent behaves in its environment.
As a solution, we consider combining two techniques with complementary benefits and drawbacks, namely reinforcement learning and reactive synthesis, that will enable to learn policies with formal guarantees.
Controller design in complex environments
Reinforcement Learning (RL) is a machine learning paradigm that allows autonomous agents that interact with an environment to learn a control policy. The idea behind RL is simple: at each step, the agent performs an action, and it receives in response a reward along with the observation of the next environment’s state.
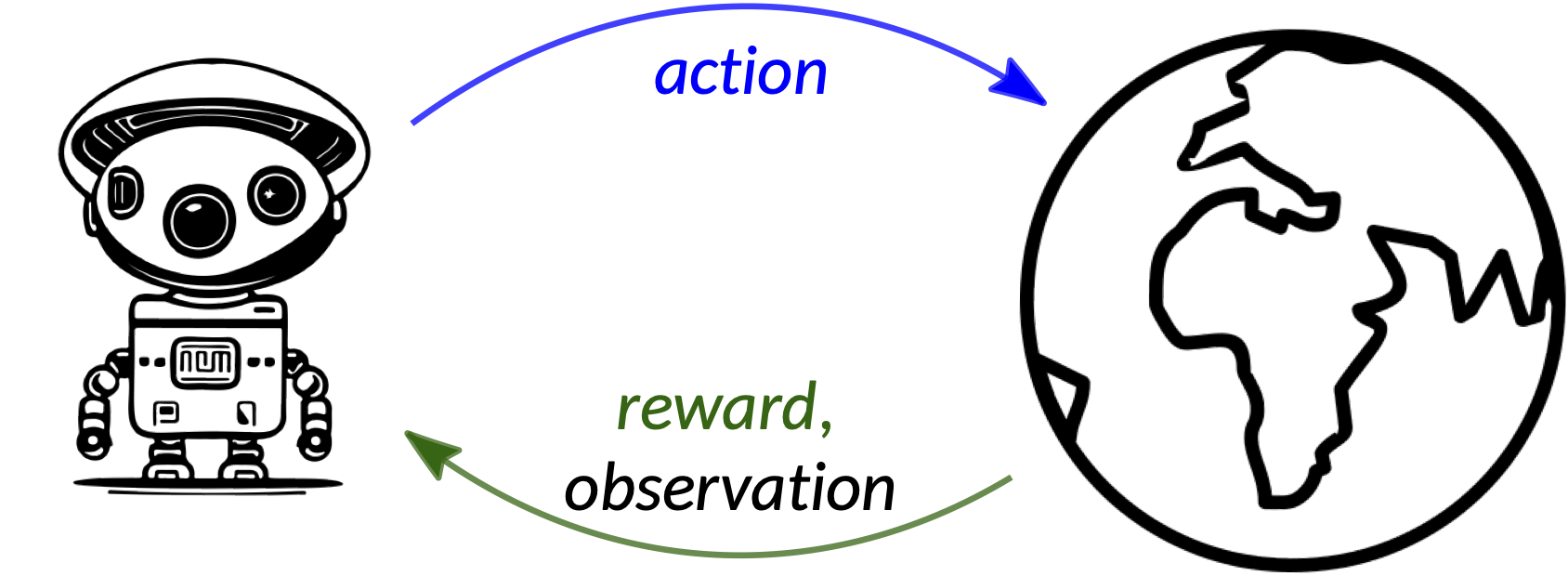
In critical applications such as epidemic control, robotics, multi-energy systems, controlling tokamak plasmas for nuclear fusion, and controlling stratospheric balloons, RL has shown great promise in enabling agents to learn efficient policies. However, deploying RL in complex, real-world systems often hits two major challenges:
- Designing a reward function that aligns the user’s intentions with the actual agent’s behaviors constitues a challenging engineering task (referred to as reward engineering).
- In general, RL lacks from formal guarantees on the induced agent’s behaviors, which raises reliability concerns, especially in high stakes scenarios.
On the other hand, when a model of the environment is available, one can apply a formal verification technique called reactive synthesis to produce controller policies with formal guarantees.
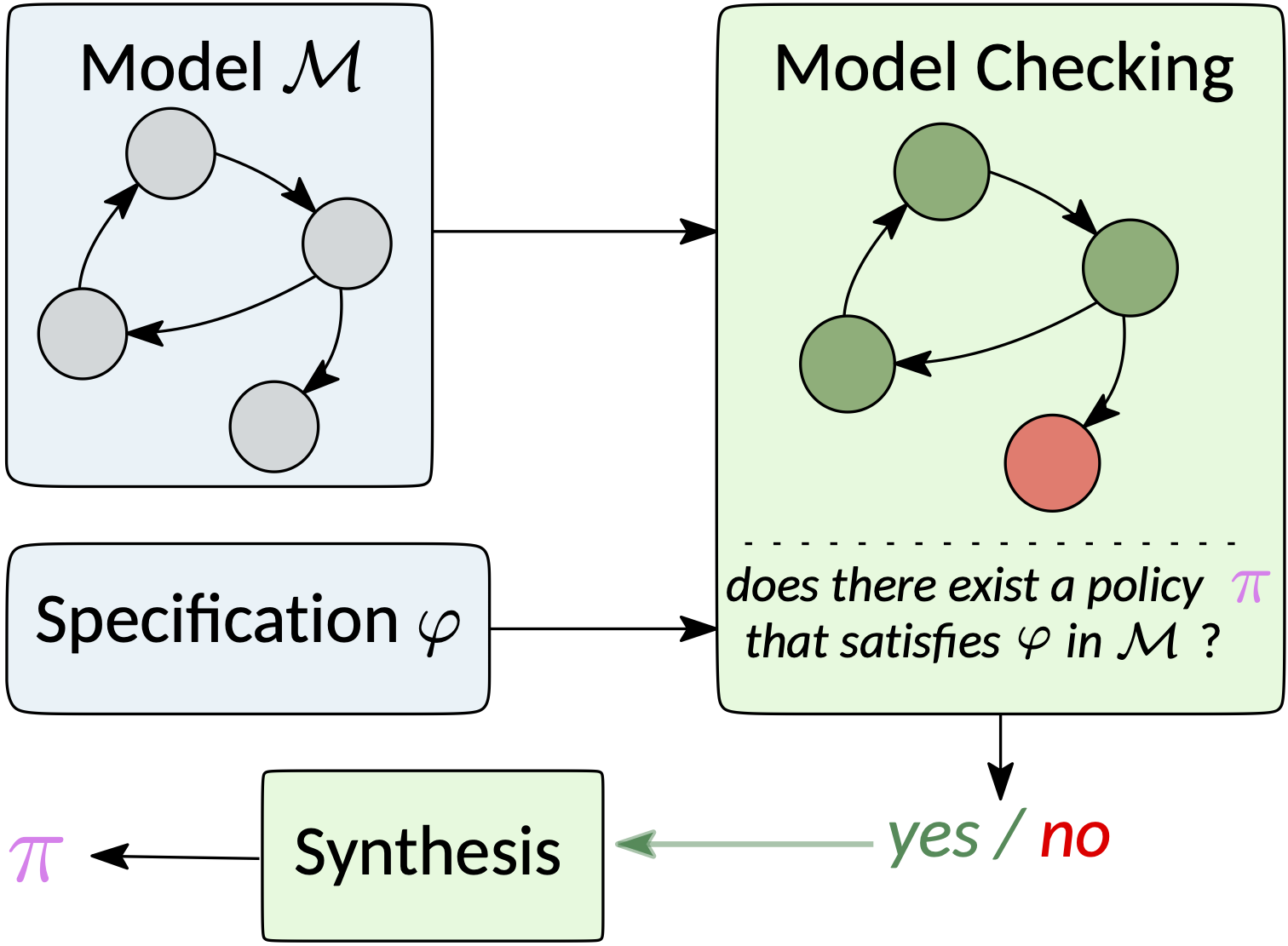
However, as mentioned, reactive synthesis relies on a user-provided model of the environment.
- this model is in fact rarely explicitely accessible (that is, under the form of a state-transition system or Markov model).
- even when it is, as model checking exhaustively explores the model (often assumed finite), it struggles to scale to large domains, and even turns intractable in complex settings.
The complement benefits and drawbacks of RL and reactive synthesis are summarized in the following table.
| Aspect | Reactive Synthesis | Reinforcement Learning |
|---|---|---|
| Model Dependency | Requires prior environment model | No prior model needed (simulating the environment is sufficient) |
| Guarantees | Formal guarantees | No formal guarantees |
| Specification | Logical formulas (intuitive, high-level) | Reward functions (engineering-intensive) |
| Scalability | Limited by the model size | Scalable to high-dimensional feature spaces (deep RL) |
Our goal is to combine the two techniques to unify their advantages while mitigating their drawbacks.
The Approach
To recap, we would like to construct controller policies for agents interacting with very large environments, with formal guarantees by combining RL and synthesis techniques. Synthesis requires some knowledge of the environment, so we consider decomposing the complex environments in two levels:
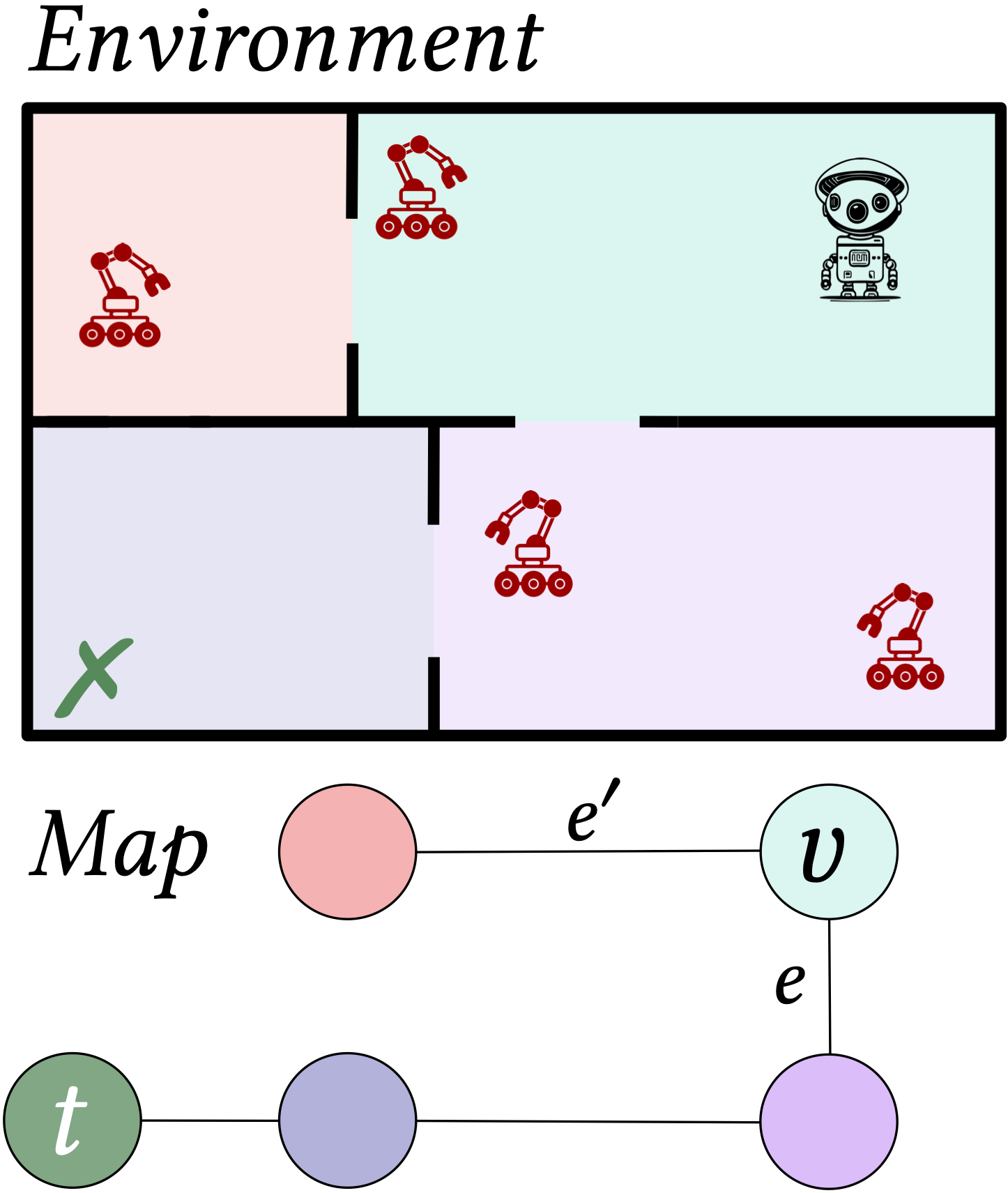
- A top-level that consists of a map provided as a graph, describing the known high-level structure of the environment. Here, we assume the user has some basic information about the environment, which is relatively easy to get.
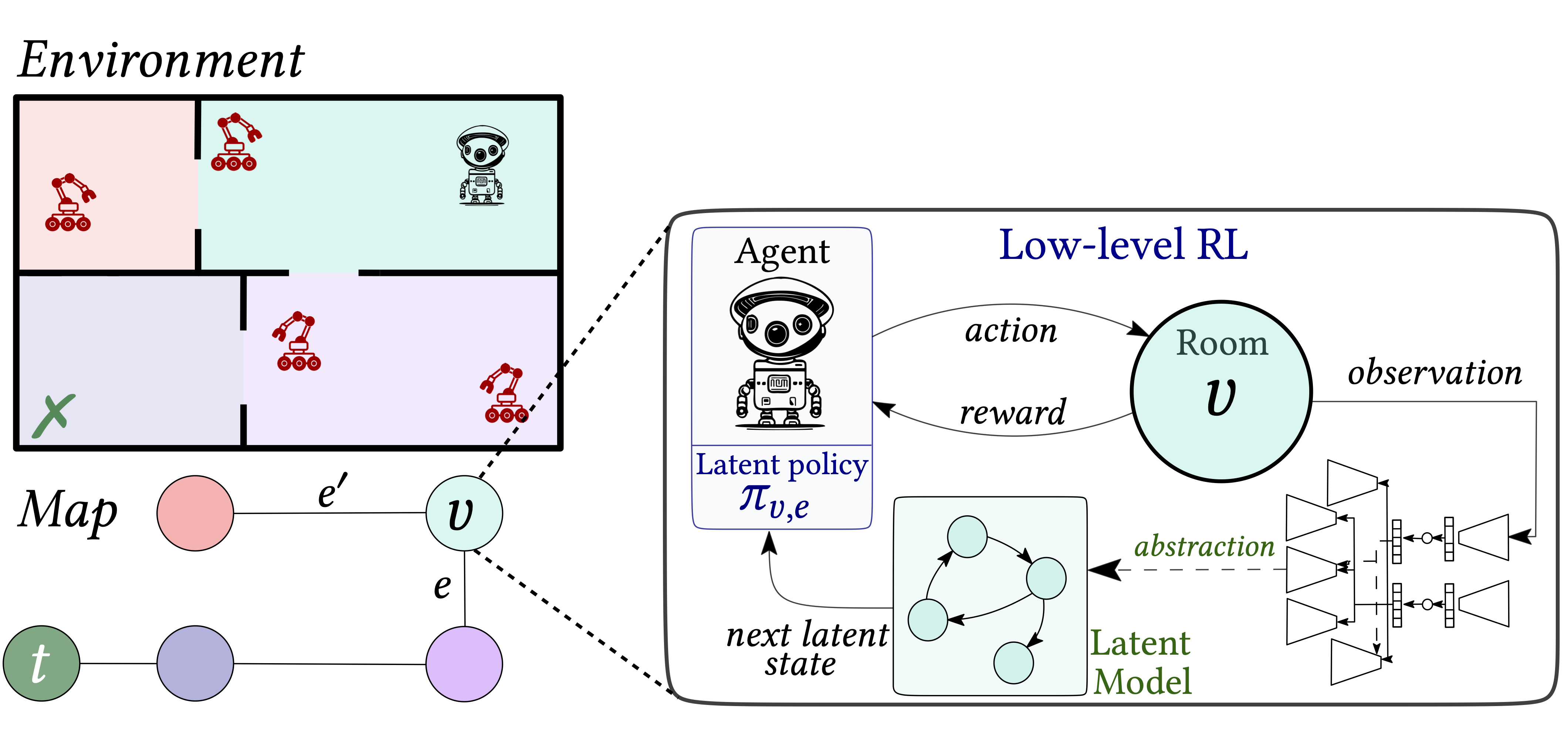
- A bottom level constitued of different “sections” that we call rooms. Concretely, we consider that each vertex of the high-level graph is populated by a Markov decision process (MDP, for short) for which the dynamics are unknown, i.e., the user doesn’t need to explicitely model each room.
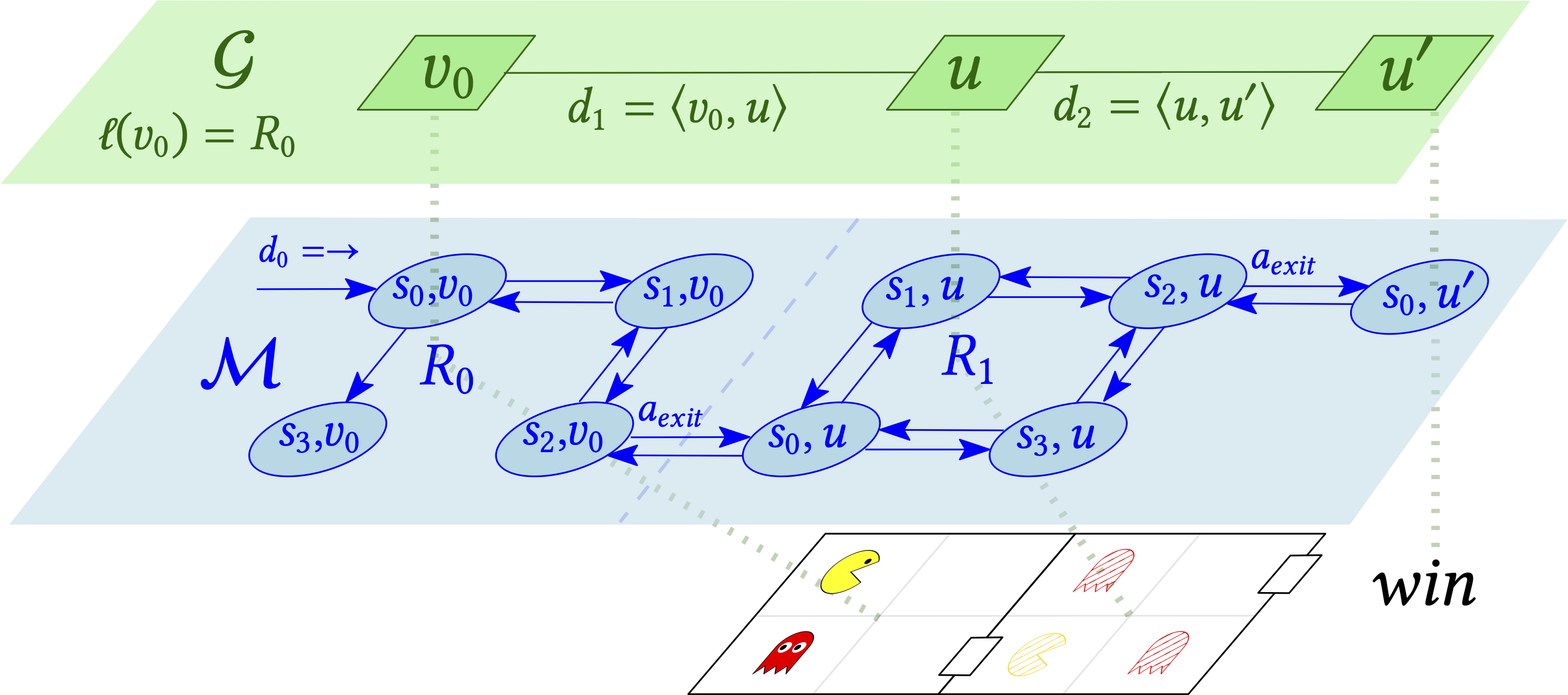
Schematic view of a two-level model. Bottom: the environment; Top: the map; Middle: unknown environment dynamics, modelled as MDPs stitched together, one for each room.
From now on, we focus on reach-avoid properties as they are the building blocks for verifying more complex specification (you may refer to this paper if you’re further interested).
Back to our warehouse example, modeling all possible interactions the agent can have with its surroundings is complicated, but providing a map of the building is straightforward.
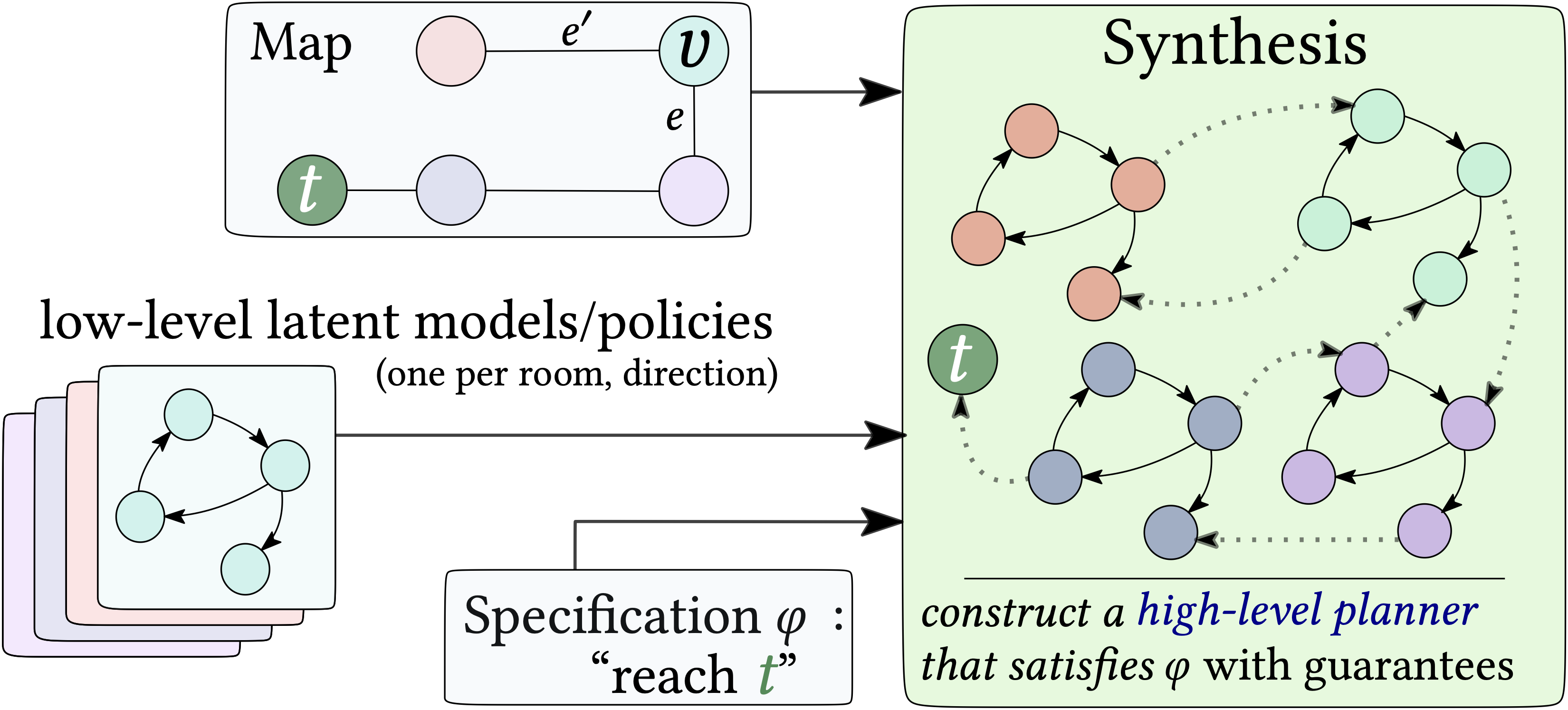
First, we apply RL in parallel in each room, and for every possible exit direction, to obtain a set of low-level policies.
Then, given the map, the set of low-level latent models and policies and a high-level specification, which consists here of reaching the target goal
The Formal Guarantees
As I mentioned above, the key advantages of our approach consist of
- the separation of concerns (reward engineering is only applied locally, in the rooms)
- the formal guarantees associated with the synthesized, two-level controllers.
Specifically, our formal guarantees are the following.
- Learning guarantees for low-level policies: the latent models of the rooms are guaranteed to be accurate abstractions. The quality of the abstraction can further be verified, and quantified through a score, formalized as probably approximately correct bounds on the loss function used to train the latent models.
- Guarantees on the synthesized two-level controller: a small amount of memory for the high-level planner is necessary and sufficient for optimal control with respect to the policies learned via RL. Furthermore, such an optimal planner can be obtained by solving an MDP obtained by stitching the latent models together.
- Unified learning and synthesis guarantees: the learning guarantees for the low-level policies (1) can be lifted to the two-level controller.
To ellaborate further on those guarantees, we need to go into a bit more details about what happens when the agent learns its low-level policies. Before describing how low-level policies are trained, let me formally introduce the concept of value function. This is a really important concept, as it’s on which our formal guarantees rely.
Value functions for discounted properties
Intuitively, given a reach-avoid specification
- the expectation is taken over the agent’s trajectories
Let’s take a closer look at this equation.
Essentially, a “payoff” of
- for computational reasons; discounting stabilitzes learning and helps handle infinite horizon properties, which otherwise simply hamper learnability
- for its compliance with RL
- for the semantics of the discount — it implicitly adds a timing aspect to the specification, which prioritizes faster satisfaction.
But most importantly, discounted valued properties tie to bisimulation metrics, ensuring latent models abstract rooms with high fidelity. We detail these guarantees below.
Low-level RL
Concretely, the low-level RL procedure consists of the following steps:
A low-level policy
An abstract latent model
The value of the policy
All low-level policies/models are learned in parallel.
For each room
 of $\mathbf{P}$ by $\phi$._](/post/composing_rl/transition_loss.png)
Finally, we showed that constructing a “compressed MDP” using the map’s structure (graph topology) and the values of the low-level specifications as transition probabilities is sufficient for optimal control with respect to the learned policies. Solving this MDP allows obtaining the high-level planner. Importantly, we proved that minimizing each individual room’s loss ensures the compressed MDP’s planner values align with the global two-level objective! So, the guarantees obtained when learning the low-level policies can be lifted to the high-level planner.
Case studies
To evaluate our approach, we considered scenarios involving an agent navigating amid moving obstacles, in a large grid world and a custom Doom environment with visual inputs. Note that both state spaces are gigantic. In the grid world, each room has size 20x20 cells and contains different obstacles/items. The grid world’s observation consists of a bitmap representing the current room (with one dimension per item/obstacle/adversary type). For ViZDoom, a game frame is provided with additional info, such as the player’s velocity, health, angle, and ammunition.
In both environments, adversaries have different (probabilistic) behaviors, and can move between rooms. In the ViZDoom scenario, random adversaries also spawn randomly in the map.


Another video of a synthesized controller for a 9x9 grid world can be found here.
With WAE-MDPs' representation learning capabilities, we only needed to train one latent model and policy per direction, which allowed us to group similar rooms together! To further emphasize low-level policies' reusability, we changed the map’s layout, increased the number of rooms (from 9 to 49), and raised the number of adversaries (from 11 to 47 in the grid world, and 8 to 20 in ViZDoom). Results are shown below.
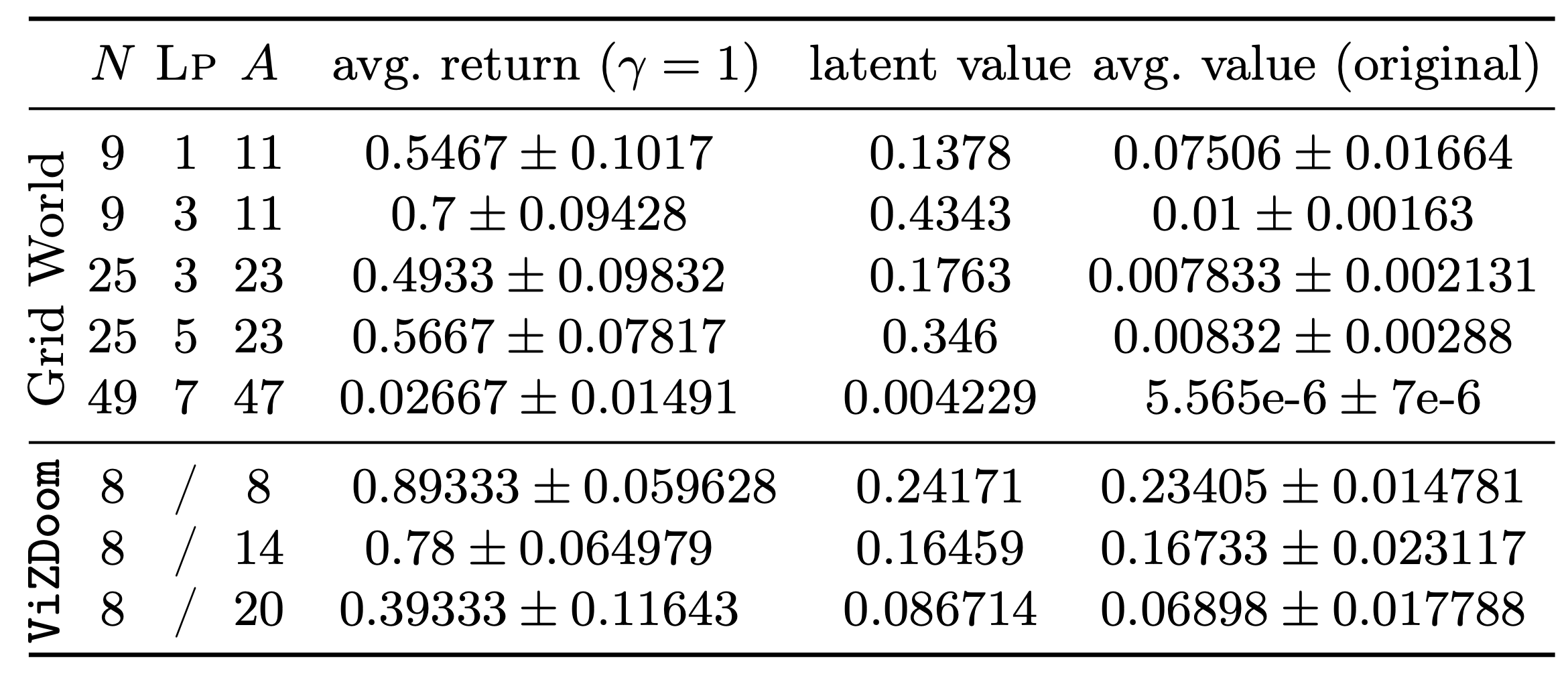
![**Table 2**: PAC bounds demonstrating the abstraction quality of the latent models learned. Each bound is evaluated for a particular policy $\pi_e$, where $e$ corresponds to the direction in which the policy is applied in the rooms. In short, the numerical values presented in the table range in the interval $[0,1]$ and gives an **_abstraction score_**. The lower the score, the more accurate the abstraction of the latent model learned is guaranteed.](/post/composing_rl/35.png)
- our two-level controllers achieve high success probability, demonstrating that our approach alleviate reward engineering issues (e.g., dealing with sparse rewards)
- the values predicted in the latent model are consistent and even close to those observed in models where the abstraction loss is proven to be low (here, in ViZDoom; see Table 2).
Discussion
In summary, we showed that carefully composing RL policies enable the application of reactive synthesis techniques to get formally verified controllers. We don’t know of any other synthesis techniques which can deal with such large environments under the same assumptions. Furthermore, our technique also allows providing controllers in domains where standard RL struggles due to the need of extensive reward engineering (e.g., because of sparse rewards). Guarantees are critical in high-stakes scenarios, and we believe drawing on ideas from and incorporating formal verification into RL is an important direction for improving the reliability of learning agents.